| verkleinert | original | vergrößert |

| 
|  |
Inhaltsverzeichnis
Einleitung
1. Physikalische Eigenschaften
1.2 Zusammenhang zwischen Farbton und Sättigung
Hauptthemen
4.2 Verlustbehaftete Codierung
5.4 Diskrete Kosinus Transformation
6. Bildkompression am Beispiel JPG
6.3 Verlustbehaftete Codierung
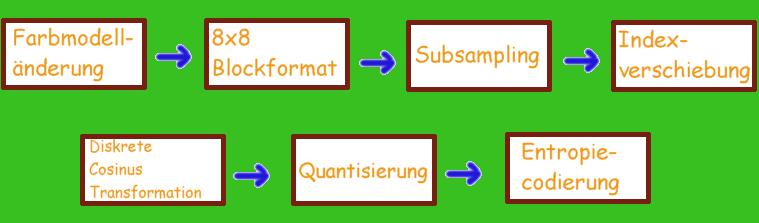
6.4.1 Änderung des Farbmodells
6.4.5 Diskrete Kosinus Transformation (DCT)
6.4.6 Quantisierung (Normalisierung)
9. Vergleich zwischen den Formaten
Schlussanmerkungen
Was ist überhaupt ein Bild? Zunächst übermittelt ein Bild Informationen wie Farbe und Helligkeit. Bei Videoübertragung kommt als zusätzliche Dimension die Zeit dazu. Im Gegensatz zum digitalen Bild liegt bei einem analogen Foto die Information fast kontinuierlich vor, sieht man mal von der endlichen Körnung des Fotopapiers ab. Der Abendhimmel auf einem Urlaubsfoto hat also im Prinzip unendlich viele Schattierungen von Blau. Durch die Aufteilung des analogen Bildes in regelmäßige Bereiche entsteht das digitale Bild. Dabei wird je nach Auflösung jeder Blauschattierung des Urlaubshimmels ein bestimmter Farbwert zugeordnet.
Angenommen, ein Bild mit einer Größe von 1000x1000 Pixeln (Breite mal Höhe) hat ein Byte pro Farbkomponente. Die Farbtiefe beträgt mit den drei Farbkomponenten demnach 24 Bit (insgesamt 16,7 Millionen Farbtöne), dies ist die übliche Auflösung. Die Größe der Bilddatei wächst schnell mit steigender Auflösung und Farbtiefe: drei MByte wollen für dieses Bild bereits gespeichert sein (1000 x 1000 x 24 = 24.000.000 bits = 3 MB).
Das RGB-Modell ist ein additives Farbmodell, d.h. mischt man die drei Farben Rot, Grün und Blau mit bestimmten Intensitäten zusammen, so ergibt sich die Farbe Weiß. Beim RGB-Modell werden die darstellbaren Farben als Punkte eines im Ursprung eines Kartesischen Koordinatensystems liegenden Einheitswürfels beschrieben. Auf den positiven Achsen dieses Koordinatensystems werden die drei Primärfaben Rot, Grün und Blau aufgetragen. Die Hauptdiagonale des Einheitswürfels, sie geht vom Punkt (0,0,0) zum Punkt (1,1,1), enthält die Farben mit gleich großem Anteil an allen Primärfarben. Sie repräsentiert die Grauwerte, wobei Schwarz im Ursprung (0,0,0) und Weiß im Punkt (1,1,1) liegen. Eine Farbe wird dann durch die Anteile an den drei Primärfarben beschrieben, die zur Farbe Schwarz addiert werden.
Das RGB-Modell ist wichtig bei der Farbdarstellung auf Monitoren. Bei Farbbildschirmen werden drei Phosphorarten auf der Mattscheibe aufgebracht, die von drei unabhängigen Elektronenkanonen angesteuert werden und das in drei Teilbilder (RGB) zerlegte Farbbild erzeugen. Daraus ergibt sich die besondere Bedeutung des RGB-Modells: alle anderen Farbbeschreibungen müssen vor der Farbausgabe in den äquivalenten Punkt des RGB-Würfels umgerechnet werden. Benutzen zwei Farbbildschirme Kathodenstrahlröhren mit verschiedenem Phosphor, so ergeben sich auch unterschiedliche Farbskalen. Man kann jedoch durch eine Transformationsrechnung die auf einer Kathodenstrahlröhre spezifizierte Farbe auf die Farbskala der anderen Röhre abstimmen.
Das CMY-Modell (Cyan, Magenta, Yellow) ist ein subtraktives Farbmodell. Dies bedeutet, dass die Mischung der Farben Cyan, Magenta und Gelb zusammen Schwarz ergibt. Bei der Darstellung der Farben in einem Kartesischen Koordinatensystem wie beim RGB-Modell liegt nun Weiß im Ursprung und nicht mehr Schwarz. Farben werden beschrieben durch die von der Farbe Weiß abgezogenen Anteile der Grundfarben und nicht mehr durch deren Addition zur Farbe Schwarz. Das CMY-Modell wird zur Farbausgabe auf Druckern verwendet, es entspricht dem physikalischen Vorgang der Reflexion weißen Lichts. Die beim Dreifarbendruck auf das Papier gebrachte Farbe sorgt dafür, daß bestimmte Farbanteile des Weißen Lichts ausgefiltert und somit nicht mehr reflektiert werden. So verhindert zum Beispiel die auf das Papier aufgetragenen Farbe Cyan, daß rotes Licht von der Oberfläche absorbiert wird. Reflektiert wird somit noch der Grün- und Blau-Anteil des Lichts. Die Druckfarbe Magenta absorbiert Grün und gelbe Druckfarbe absorbiert Blau. Werden Cyan und Gelb nun übereinander auf das Papier aufgetragen, so wird nur der Grün-Anteil des anstrahlenden Lichts reflektiert. Werden alle drei Farben auf das Papier aufgetragen, dann werden Rot, Grün und Blau absorbiert und man erhält so die Farbe Schwarz. Beim Farbdruck wird jedoch häufig zusätzlich schwarze Tinte eingesetzt, da sie ein dunkleres Schwarz liefert als man es durch die Mischung der drei Grundfarben erhalten würde, und da der Trockenvorgang durch die reduzierte Menge an Cyan-, Magenta- und Gelb-Tinte beschleunigt wird. Die Umrechnung zwischen RGB- und CMY-Modell erfolgt nach folgenden Formeln:[C,M,Y] = [1,1,1] - [R,G,B] bzw. [R,G,B] = [1,1,1] - [C,M,Y]
Beim YUV-Modell (wird beim Farbfernsehen verwendet) steht Y für die Luminanz (Helligkeit), U und V beschreiben die Chrominanz (Farbigkeit). U beschreibt den Farbton und V die Farbsättigung. Das YUV-Format wird verwendet, da die hier gespeicherten Werte der Wahrnehmungsfähigkeit des menschlichen Auges besser entsprechen. Das menschliche Auge kann örtliche Helligkeitsunterschiede sehr viel besser auflösen und unterscheiden als Farbänderungen, so daß die voneinander unabhängigen Y- und UV-Werte mit unterschiedlichem Kompressionsverhältnis reduziert werden können. Hinzu kommt, daß Bildregionen mit gleicher Helligkeit oder gleicher Farbsättigung wesentlich häufiger sind als Bildregionen mit gleichen Anteilen an Rot, Grün und Blau. Im YUV-Format haben daher weite Strecken der Pixeldaten, insbesondere für die Helligkeit, gleiche oder ähnliche Werte. Solche Strecken lassen sich wesentlich stärker komprimieren, als Daten, in denen sehr viele verschiedenen Werte vorkommen.
Die Farbe wird durch den Farbton bestimmt. Er besagt, ob es sich z.B. um einen Blauton, Grünton oder Gelbton handelt. Der Grauanteil einer Farbe wird durch die Sättigung bestimmt. Wird beispielsweise die Sättigung verringert, so erhöht sich der Grauanteil. Bei keiner Sättigung erscheint jede Farbe als Grau. Farben mit nur einem sehr geringem Sättigungsgrad bezeichnet man auch als trübe Farben. Erhöht man den Sättigungsgrad, so erscheint eine Farbe reiner. Der Begriff Helligkeit erklärt sich selbst. Ohne Helligkeit wird jeder Farbton zum Schwarz, und mit maximaler Helligkeit wird jeder Farbton zum Weiß.
Digitale Bilder werden auf dem PC meistens durch Bitmaps repräsentiert. Eine Bitmap ist eine Matrix mit der Breite b und der Höhe h von Punkten, sie enthält insgesamt b x h Punkte (man nennt diese Punkte auch picture elements, kurz Pixel). Pixelformate teilen ein Bild in Zeilen und Spalten auf und speichern den Farbwert jedes Bildpunktes.
Grundsätzlich unterscheidet man zwischen zwei verschieden Bitmaptypen:
Verkleinerung: Interferenzmuster (Überlagerungen)
Vergrößerung: Blockstrukturen an Rändern
farbige Bitmap:
| verkleinert | original | vergrößert |

| 
|  |
monochrome Bitmap

|
Für manche Bereiche sind Vektorgrafiken jedoch ungeeignet. Will man zum Beispiel ein Foto in den PC einscannen, so erzielt man mit Bitmapgrafik normalerweise bessere Ergebnisse, als wenn man den Inhalt des Fotos durch geometrische Objekte beschreibt. Schließlich gibt es in der Natur keine perfekten Kreise, Dreiecke, Rechtecke usw.
Gerade im Bereich der digitalen Bildverarbeitung dominiert die Bitmapgrafik, während bei den technischen Zeichnungen fast nur die Vektorgrafik zum Einsatz kommt. Die Datei besteht also aus mathematischen Beschreibungen der dargestellten Bildelemente (Rechtecke, Linien, Kurven, Flächen, Körper...). Vektorformate speichern die Parameter der im Bild enthaltenen graphischen Elemente, z.B. die Position und den Umfang eines Kreises, sowie die Breite der Linien und deren Farbe. Dafür ist eine Vektorgrafik-Datei oft wesentlich kompakter als eine Bitmap-Datei, kann aber manchmal auch um einiges größer sein, abhängig von der Komplexität der math. Beschreibungen.

Veränderungen von Größe, Farbe und sonstigen Eigenschaften können ohne Qualitätsverluste vorgenommen werden.
Wichtige (oder besser: bekannte Formate) sind: BMP, TIF, PCX, GIF, TGA, PNG, JBIG
Hier sind die wichtigsten Formate: JPG, FIF, WA
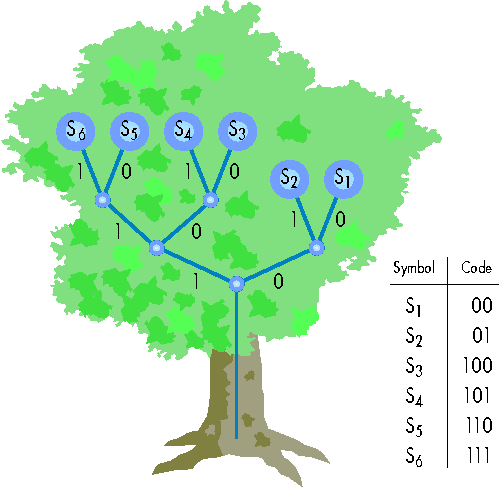
Nach Huffman ordnet man alle Symbole zunächst nach ihrer Häufigkeit in einer Tabelle. Die beiden seltensten erhalten als letzte Codeziffer eine 0 und eine 1. Beide werden in der Tabelle mit der Summe ihrer Wahrscheinlichkeiten zusammengefasst. Die Häufigkeitstabelle hat damit ein Element weniger. Wieder sucht man die beiden seltensten Elemente und stellt ihrem Code eine 0 und eine 1 vor. Nach Zusammenfassen ihrer Wahrscheinlichkeiten beginnt das Spiel von vorn. Alle Symbole sind codiert, wenn nur noch ein Element in der Tabelle übrig ist.
Bei diesem Schema werden die Symbole zunächst in einem Intervall von 0 bis 1 angeordnet. Die Wahrscheinlichkeit eines Symbols entspricht dabei der Länge seines zugehörigen Unterintervalls. Besteht eine Datei aus zehn Symbolen, so gibt es daher zehn Unterintervalle. Je kleiner das zu einem Symbol gehörige Unterintervall ist, desto länger wird sein Codewort, und umgekehrt.
Die Codierung erfolgt dadurch, daß jedem Symbol eine binäre Fließkommazahl zugeordnet wird, die dem Anfang der Position des Unterintervalls entspricht. Aus den Fließkommazahlen wird mit Hilfe der Unterintervalle eine einzige Zahlenfolge gebildet, die letztlich in einen Code umgesetzt wird.
Im Vergleich zur Huffman-Codierung, die jedem Zeichen einen Code zuordnet, ist die arithmetische Codierung mit Codes für Zeichenfolgen effizienter. Leider besitzen Firmen wie IBM, AT&T und Mitsubishi die Patentrechte, so daß man eine Lizenz benötigt um diese Verfahren anwenden zu dürfen, deshalb benutzt man meist die Huffman-Codierung.
Die Transformation von RGB nach YUV erfolgt durch eine einfache Matrizenmultiplikation. Die YUV-Komponenten ergeben sich als gewichtete Summe aus den RGB-Komponenten (Y= 0,299 * R + 0,587 * G + 0,114 * B, U = - 0,169 * R - 0,3316 * G +0,500 * B, V = 0,500 * R - 0,4186 * G - 0,0813 * B). Bei dieser Transformation wird der Wahrnehmungsfähigkeit des menschlichen Auges Rechnung getragen. So wird beispielsweise wegen der höheren Empfindlichkeit des menschlichen Auges für Grün bei der Berechnung des Y-Wertes die Grünkomponente am stärksten berücksichtigt (Faktor 0,587).

Jetzt wird auf jeden dieser 8 x 8 Blöcke die zweidimensionale FDCT (Forward Descrete Cosine Transformation) angewandt. Dadurch werden die Pixelwerte aus dem zweidimensionalen Bereich in den Frequenzbereich transformiert (Spektralanalyse).
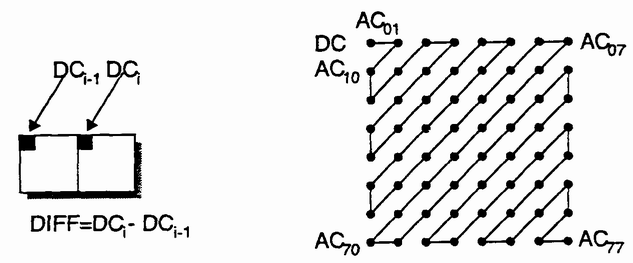
Dabei enthält der Wert in der linken oberen Ecke der 8 x 8 Matrix die niedrigsten Frequenzanteile. Dieser Koeffizient an der Stelle (0,0) wird normalerweise als DC-Koeffizient (Gleichstromkoeffizient), die anderen 63 Koeffizienten als AC-Koeffizienten (Wechselanteile) bezeichnet. Da normalerweise ein starker Zusammenhang zwischen den DC-Koeffizienten zweier aufeinander folgender 8 x 8-Blöcke existiert, wird der DC-Koeffizient als Differenz zum Vorgänger codiert. Die restlichen 63 AC-Koeffizienten werden entsprechend dem Zick-Zack-Muster sortiert.
Die DCT konzentriert die Signalenergie eines Blockes in den 'niedrigen' Koeffizienten, vor allem im DC-Koeffizienten. Die höheren AC-Koeffizienten sind meist 0 oder fast 0, da der überwiegende Anteil der visuellen Information eines Bildes mit kontinuierlich verteilten Werten im Bereich niedriger Frequenzen liegt. Der Grundgedanke dabei ist das in einem natürlichen Bild (Foto, etc.) scharfe Kanten, Linien, abrupte Farbwechsel etc. eher selten sind. Daher ist der Unterschied zwischen 2 benachbarten Farbpunkten meist sehr gering. Deshalb konzentriert sich der größte Teil des Ausgangssignals in den unteren Frequenzen.
Sieht man von der Rechenungenauigkeit bei Matrizenmultiplikation und DCT ab, so ist bis auf das optionale Subsampling, das für das menschliche Sehvermögen unwesentlich ist, das Verfahren bisher nicht verlustbehaftet und noch umkehrbar. Allerdings hat man bis auf das Subsampling bisher auch keine Reduzierung der Daten erreicht, sondern diese nur für eine Kompression optimiert.
Die Quantisierung ist der eigentliche verlustbehaftete Prozess beim JPEG-Algorithmus. DCT Koeffizienten, die sich nicht wesentlich voneinander unterscheiden, werden zu einem Wert zusammengefasst. Dies geschieht, indem man alle Matrizenwerte durch eine vorgegebene Schrittweite dividiert. Erlaubt ist auch, daß der Anwender selbst in den Vorgang der Quantisierung eingreifen kann. Durch Wahl der Quantisierungsschritte kann er so sein Optimum für das Verhältnis Speicherplatz / Bildqualität finden.
Hilfe einer Quantisierungstabelle werden die Ergebniswerte der DCT in Stufen eingeteilt. Das JPEG-Komitee hat solche als Richtlinien vorgegeben. Dabei werden kleine Werte feiner quantisiert (höher bewertet) als größere Werte, um den Informationsverslust klein zu halten.
Neben der Verkleinerung des Wertebereichs erreichte man, daß noch weitere Koeffizienten höherfrequenter Funktionen zu Null geworden sind. Die Art der Quantisierung ist von JPEG nicht vorgeschrieben. Oft erfolgt die Quantisierung mit Hilfe so genannter psychovisueller Gewichtsfunktionen. Diese berücksichtigen die Farb- und Helligkeitsempfindlichkeiten des menschlichen Auges und sehen für unterschiedliche Frequenzen unterschiedliche Quantisierungsschrittweiten vor.
Nach der Quantisierung wird der DC-Anteil getrennt von den AC-Teilen behandelt. Weil zwischen den DC-Koeffizienten benachbarter 8x8-Blöcke eine hohe Korrelation herrscht, werden diese nur als Differenz zum vorhergehenden Block codiert. Die AC-Koeffizienten werden in einem Zickzackkurs aufgereiht. Durch diese Abtastung der Matrix erreicht man, daß die Nullwerte zu zusammenhängenden Abschnitten zusammengefaßt werden.
Die Dekodierung erfolgt in umgekehrter Reihenfolge
Die Ähnlichkeit zwischen Domain- und Range Block muss nicht offensichtlich sein, sondern stellt sich oft erst nach Transformationen wie Spiegelung oder Streckung ein. Insgesamt gibt es acht Typen dieser affinen Transformationen. Mit dazu gehören Spiegelungen und Rotationen. Jeder Domain Block wird unter Anwendung dieser acht Transformationen mit jedem Range Block verglichen. Da jedoch zwei Blöcke selten perfekt übereinstimmen, wird zusätzlich die Distanz (als Quadratsumme der Differenz korrespondierender Pixel) zwischen Domain- und transformierten Range Blocks berechnet. Zwei Blöcke passen dann zueinander, wenn die Distanzwerte zwischen ihnen am geringsten sind. Das transformierte Bild besteht am Ende aus vielen mathematischen Gleichungen, welche die fraktalen Teilbilder darstellen.
Für die Bildung der Domain Blocks und die Vergleichsmethodik gibt es allerdings viele verschiedene Verfahren. Die Suche nach dem besten Verfahren ist noch Gebiet der Forschung. Die existierenden Strategien bieten allerdings schon hohe Kompressionsraten bei Realbildern und Schwarzweißgraphiken.
Die Vielzahl der Vergleiche bei allen diesen Verfahren erfordern allerdings viel Zeit bei der Codierung. Anfangs dauerte ein fraktaler Kompressionsprozess Stunden bis Tage, mittlerweile schaffen das clevere Algorithmen in Minuten. Die Dekompression ist dagegen rasend schnell: In weniger als 16 Iterationen ist die Bildrekonstruktion abgeschlossen. Die Transformationen werden in umgekehrter Richtung abgearbeitet, indem das Bündel mathematischer Gleichungen immer wieder auf das Bild angewendet wird. Dadurch stellt sich das ursprüngliche Verhältnis von Domain zu Range Blocks wieder ein. Dieses Verfahren wird so lange wiederholt, bis das nach einigen Iterationen erzeugte Bild sich nicht mehr vom Ergebnis der nächsten Iteration unterscheidet.
Die Wavelet-Transformation zerlegt das Bild in hoch- und tiefpaßgefilterte Anteile. Nach einer Iteration steckt die wesentliche Bildinformation im tiefpaßgefilterten Teilbild, da auch hier der größte Teil der Bildinformation in den niedrigen Frequenzen liegt. Auf dieses Teilbild wird das Verfahren dann erneut angewendet.
Die Filterpaare teilen die Bandbreite des Bildes in zwei Hälften, die eine hoch-, die andere tiefpaßgefiltert. Beide Hälften sind so beschaffen, daß sich bei beiden Bildern jeweils jede zweite Pixelspalte entfernen lässt. Das Ergebnis: zwei insgesamt "schmalere" Bilder.
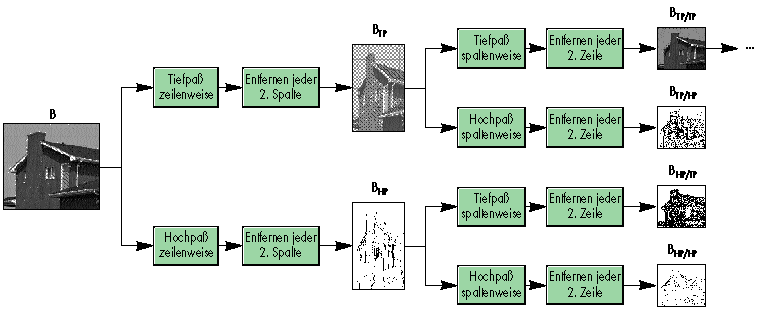
Die gleiche Filterung wird nochmals auf die beiden Bilder angewendet, jetzt allerdings entlang der Vertikalen. Am Ende liegen dann vier gefilterte Bilder vor. Statt jeder zweiten Spalte kann nun jede zweite Zeile entfernt werden. Aus dem Ausgangsbild sind vier verkleinerte Bilder entstanden, wobei eines davon eine Sonderstellung einnimmt: Dieses eine Bild entspricht dem Durchschnittssignal, die anderen drei sind dagegen Detailsignale. Das Durchschnittssignal-Bild läßt sich genauso weiter transformieren und reduzieren - theoretisch so lange, bis es nur noch ein Pixel groß ist. Das ist allerdings nur möglich, wenn die Kantenlängen des Bildes Zweierpotenzen sind. Da das im Allgemeinen nicht der Fall ist, ist es praktischer, bei einer bestimmten Iteration aufzuhören.
Nach dieser Wavelet-Transformation in Vorwärtsrichtung liegen die Teilbilder in Form einer Matrix von Koeffizienten vor.
Die eigentliche Kompression erfolgt dann wie bei JPEG im Quantisierungsschritt. Verschiedene Strategien fassen dabei unwichtige Bilddetails zusammen, sofern man nicht gleich auf sie verzichtet. Koeffizienten mit Werten nahe Null werden je nach Toleranzschwelle gelöscht. Nach einer anschließenden Codierung, zum Beispiel mit dem Huffman-Verfahren, liegt das Ergebnis vor. Dieses Verfahren arbeitet im Gegensatz zu allen anderen hier vorgestellten Codierungen global, teilt das Bild also nicht in Blöcke auf. Um aus den Daten wieder ein Bild zu erhalten, werden alle Schritte in umgekehrter Reihenfolge, mit denselben gespiegelten Hoch- und Tiefpaßfiltern ausgeführt.
Ein Aspekt dabei, der sich vor Allem bei der Netzübertragung positiv auswirkt ist, daß sehr schnell ein grobes Bild vorhanden ist, dessen Qualität sich während der Datenübertragung stetig verbessert.
Die Vielzahl der möglichen Grundwellenformen bewirkt allerdings auch hier, wie bei der Fraktalen-Codierung, daß die Suche nach der besten Methode sehr schwierig ist und ein wirkliches Optimum wahrscheinlich nie gefunden wird. Bei geeignetem Wavelet und Filtern ergeben sich allerdings schon jetzt bessere Kompressionsraten, als bei JPEG.
| Format | Tagged Image File Format | Portable Network Graphics | Graphic Interchange Format | JPEG | Fraktal | Wavelet |
| Codiermethode | verlustfrei | verlustfrei | verlustfrei | verlustbehaftet | verlustbehaftet | verlustbehaftet |
| Strategie der verlustbehafteten Formate | Blocking | Blocking | Non-Blocking
Blocking möglich |
|||
| bevorzugtes Bildermaterial | alle | alle | abstrakte Bilder, da nur bis 256 Farben möglich | Realbilder in Echtfarben | Realbilder | alle |
| Endung | TIF | PNG | GIF | JPG | FIF | WA |
| Kompressionsrate | niedrig | hoch | bis 5:1 | bis 20:1 und 25:1 gut, danach deutliche Artefakte | auch bei sehr hohen Kompressionsraten gut | auch bei sehr hohen Kompressionsraten sehr gut |
| Zeitverhalten | symmetrisch | symmetrisch | symmetrisch | symmetrisch | asymmetrisch
Kompression langsam, Dekompression sehr schnell |
symmetrisch |
| Methode | LZW | LZW | LZW | DCT | iterierte Funktionssysteme | versch. Basisfunktionen und Filtertypen |
| Subformate | Interlaced PNG | Animated GIF
Interlaced GIF |
Progressive JPG
Hierarchial JPG Motion JPG |
Es werden folgenden Verfahren verglichen :
Das Originalbild: lena
| Kompressionsfaktor | Diskrete Kosinus- Transformation (DCT) | Wavelet- Transformation | Fraktale Kompression |
|---|---|---|---|
| 1:10 | lena10 | lena10 | lena10 |
| 1:15 | lena15 | lena15 | lena15 |
| 1:25 | lena25 | lena25 | lena25 |
| 1:35 | lena35 | lena35 | lena35 |
| 1:50 | lena50 | lena50 | lena50 |
| 1:100 | lena100 | lena100 | lena100 |
Anhand der resultierenden Bilder kann man zunächst folgendes erkennen:
| Kompressionsfaktor | Diskrete Kosinus- Transformation (DCT) | Wavelet- Transformation | Fraktale Kompression |
|---|---|---|---|
| SNR in dB / RMS | SNR in dB / RMS | SNR in dB / RMS | |
| 1:10 | 36.4 / 3.84 | 38.3 / 3.09 | 36.2 / 3.97 |
| 1:15 | 35.1 / 4.48 | 36.4 / 3.85 | 33.8 / 5.19 |
| 1:25 | 32.9 / 5.74 | 34.3 / 4.94 | 31.4 / 6.86 |
| 1:35 | 30.4 / 7.70 | 32.8 / 5.86 | 29.6 / 8.41 |
| 1:50 | 27.3 / 10.97 | 31.3 / 6.95 | 27.4 / 10.90 |
| 1:100 | 24.2 / 15.78 | 28.6 / 9.47 | 22.2 / 19.74 |
H.261 beruht auf einer Hybridkodierung (Verwendung mehrerer Codierverfahren) aus der bei JPEG beschriebenen Diskreten Kosinus Transformation (DCT) und der Differenziellen Puls Code Modulation (DPCM).
Durch die Prädiktionstransformation entsteht eine Matrix gleicher Dimension, deren Werte aber nur eine kleine Varianz aufweisen, so daß eine abschließende Entropiecodierung höhere Kompressionsraten erzielen kann.
MPEG sollte eine Weiterentwicklung des H.261-Standards sein, die bei besseren Übertragungsraten eine erheblich bessere Qualität bietet und auch asymmetrische Videoanwendungen, d.h. Filme, die einmal mit einigem Aufwand codiert und oft wiedergegeben werden, unterstützt. Beispiele hierfür sind Unterhaltungsvideos, Präsentationen, Animationen in Lexika, etc.
Das Ziel der stufenweisen Entwicklung von aufeinander aufbauenden Standards waren hauptsächlich die unterschiedlichen Anforderungen von Video- und Fernseh-Anwendungen. So wurde MPEG-1 für CD-ROM Video-Anwendungen mit Datenraten um 1,5 Mbit/s optimiert. MPEG-2 wurde dann entworfen für Anwendungen in der Fernsehtechnik bei höheren Übertragungsraten und einem Bildaufbau mit Zeilensprung (interlaced), dessen spezielle Eigenschaften auch besondere Verarbeitungsweisen erfordern.
MPEG-3 zielte ursprünglich auf HDTV-Anwendungen. Bei der Entwicklung von MPEG-2 wurde dann jedoch erkannt, daß die MPEG-2 Verfahren mit geringer Verbesserung ihrer Leistungsfähigkeit imstande sind, Videodaten auch von hochauflösenden Bildern gut zu verarbeiten. Daher wurde MPEG-3 in den MPEG-2-Standard eingebettet.
Neben Entwicklungen von Test- und Simulationsstandards für die bestehenden Verfahren wird im Rahmen von MPEG-4 an einer neuen Technologie gearbeitet, deren Ziel u.a. die Unterstützung folgender Anwendungen ist:
Quellenverzeichnis
c't 11/1996 S.222ff: Handlich bunt - Kompressionstechniken für Bild- und Videodaten im Vergleich
c't 26/1999 S.185ff: Schlanke Bilder - Der zukünftige Bildkompressionsstandard JPEG 2000
Ralf Pichler - Bild und Videokompression